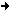For those interested in calculating how fast their rolls would be
going after some paper buildup, here are Rex Lawson's calculations from
Player Piano Group Bulletin 138 (Autumn 1996):

If C = circumference of take-up spool (and C2 is circumference squared)
   L = length of paper rolled onto spool
   c' = new circumference (and c'2 is the square)
   t = thickness of roll paper

The cross-sectional area of a take-up spool, A = pi * r * r
The circumference of the spool, C = 2 pi *  r
Therefore, C2 = 4 pi * A

Rolling a length of paper onto a spool increases the total cross-
sectional area by the cross-sectional area of the paper = Length *
thickness.

Therefore the new circumference can be calculated as

          c'2 = 4 pi (A + L*t) = C2 + 4 pi t

A standard Aeolian Duo-Art spool has circumference 6 inches.  Rolling
on 120 inches of paper of 3 thousandths thickness increases the circum-
ference to 6.36 inches, an increase of 6%.

If the take-up spool rotates at a constant number of revolutions per
minute (and does not slow down) then the paper speed over the tracker
bar is simply proportional to the spool circumference.  Hence the speed
in this case will have increased by 6 %.  If the roll speed was 80 at
the start, after 10 feet it is effectively 84.8.

As for the effect of drag slowing a roll down, I very much doubt that
many machines will have slowed by 6% after only 10 feet of paper!

Julian Dyer